Normalformer och normalisering

Det kan vara bra att läsa kursavsnittet om relationsmodellen först.

Varför ska jag lära mig det här?

Men teorin om normalisering behövs ändå:

• Det är inte alltid så lätt att inse vad de där "sakerna" som man ska ha en per rad egentligen är. Förmodligen ska en leverantör räknas som en sak. Men kan det faktum att vi köper en vara från en viss leverantör vara en sak?
• Det kan också vara svårt att avgöra vad som ska bli entitetstyper i ER-diagrammet. Är det faktum att vi köper en vara från en viss leverantör en entitetstyp eller en sambandstyp?
• Man behöver ibland analysera en existerande eller föreslagen design, och då måste man förstå, och kunna förklara, vilka problem den medför. Kanske måste man göra en avvägning mellan de nackdelar en dåligt normaliserad design medför, och arbetet att göra om databasen.

Ett förklarande exempel

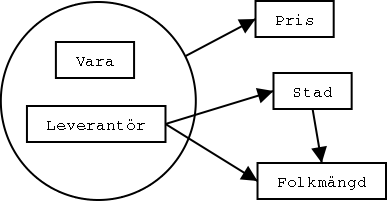
Vi vill hålla reda på vilka varor (till exempel bilar) vi köper, och från vilka leverantörer (till exempel Volvo) vi köper dem. Vi kan köpa varje vara från olika leverantörer.

Dessutom vill vi veta varornas pris. Priset för en vara är förstås olika beroende på från vilken leverantör vi köper den.

Vi vill också lagra leverantörernas adresser i databasen, dvs i vilken stad varje leverantör ligger. Vi antar nu att varje leverantör bara finns i en enda stad.

Kanske behöver vi plötsligt beställa väldigt många bilar från Volvo. Då kan det vara bra att veta hur många människor som bor i staden där Volvo ligger, så att vi vet om Volvo snabbt kan nyanställa folk för att tillverka bilarna. Därför lagrar vi folkmängden för varje stad.

Första försöket att göra en databas

Vara och Leverantör bildar tillsammans primärnyckel.

Det här är inte någon bra lösning.

• Onödig redundans. Vissa saker lagras på flera ställen, till exempel att Saab ligger i Södertälje. Det tar förstås onödig plats, och det är dessutom lätt att man får motsägelser i databasen, om man till exempel ska göra en ändring och glömmer att ändra på alla ställen.
• Vissa saker går inte att lagra, vilket kan ge problem både vid insättning och borttagning. Antag att vi hittat en leverantör som vi vill lägga in i databasen, innan vi hunnit köpa något från det företaget. Vad ska vi då skriva i kolumnen Vara? Och om vi slutar köpa bilar från Volvo, och stryker den raden ur tabellen, så försvinner också all information om Volvo.
• Tabellen har en grötig semantik, vilket betyder att de kan vara svårt att förstå riktigt vad den betyder. Helst ska varje tabell beskriva en typ av sak, och varje rad i tabellen ska innehålla data om en sådan sak. Men vad betyder egentligen en rad i den här tabellen? Betyder den första raden att vi köper bilar från Volvo? Men vad har i så fall staden Torslanda med saken att göra? Är det i den staden som inköpet görs? Och hur är det med den där folkmängden på 80000? Är det hur mycket folk som jobbar på Volvo? Eller är det så många personer som behövs för att köra hem alla bilarna?

Enkel regel för hur tabeller ska se ut

Exempel: Om vi ska lagra information om anställda, så skapar vi en tabell som heter Anställd, och där varje rad handlar om en anställd. Vi kan till exempel ha de här kolumnerna:

• Nummer (den anställdes nummer)
• Namn (den anställdes namn)
• Telefon (den anställdes telefonnummer)
• Lön (den anställdes lön)
• Chef (vem som är den anställdes närmaste chef)
• Avdelning (den avdelning som den anställde jobbar på)
• Stad (den stad som den anställde bor i)

• Chefstelefon (telefonnummer till den anställdes närmaste chef). Den informationen hör ihop med chefen, inte med den anställde.
• Avdelningsadress (adressen till avdelningen som den anställde jobbar på) Den informationen handlar om avdelningen, inte om den anställde.
• Folkmängd (folkmängd i staden som en anställde bor i) Den informationen handlar om staden, inte om den anställde.

Ofta räcker det med det den här enkla regeln. Om man bara följer regeln om en typ av sak per tabell, en sak per rad, och en rad per sak, så kommer ens databaser att få en bra design, och man undviker problemen med redundans, saker som inte går att lagra, och tabeller som är svåra att förstå.

Men ibland är det svårt att riktigt veta vad det är för "saker" man vill lagra, och vilka data som egentligen hör ihop med dem. Då har vi nytta av teorin om normalisering. Den hjälper oss att se exakt hur de olika kolumnerna i tabellen hör ihop, och visar oss hur vi ska dela upp tabellen för att slippa problemen. Därför börjar vi nu titta på de olika normalformer som teorin om normalisering beskriver. Normalformer är villkor som en tabell kan uppfylla. Det enklaste villkoret är första normalformen, och genom att lägga på fler villkor kan man definiera andra normalformen, tredje normalformen, och så vidare.

Första normalformen, "1NF"

Eller nästan i alla fall. Det går förstås att göra ett textfält och sen stoppa in flera namn, med till exempel komma mellan dem: Saab,Volvo,Renault. Ett problem med det är att det blir ganska svårt att göra sökningar i databasen, eftersom SQL-frågorna blir krångliga. Det är inte meningen att man ska göra så, och databashanterarna är inte byggda för att klara det på ett enkelt sätt.

Funktionellt beroende, "fb"

Mer formellt kan vi säga att om värdet på ett (eller flera) attribut A entydigt bestämmer värdet på ett annat attribut B, så är B funktionellt beroende av A. "Entydigt bestämmer" betyder att om värdena på A på två rader i tabellen är lika, så måste värdena på B också vara lika. Det kan skrivas med en pil: A -> B. Vi kallar A för en determinant, eftersom den bestämmer ("determinerar") B.

I exempeltabellen finns dessa funktionella beroenden:

• Vara, Leverantör -> Pris
• Leverantör -> Stad
• Stad -> Folkmängd
• Leverantör -> Folkmängd

I fortsättningen förkortar vi ibland "funktionellt beroende" till "fb".

Fullständigt funktionellt beroende, "ffb"

Vi har sett att på varje rad där det står Södertälje i kolumnen Stad, så kommer det att stå 50000 i kolumnen Folkmängd. Detta betydde, sa vi, att kolumnen Folkmängd är fb av Stad.

Men då kan vi också säga så här:

Vi har sett att på varje rad där det står Södertälje i kolumnen Stad, och där det står Bil i kolumnen Vara, så kommer det att stå 50000 i kolumnen Folkmängd. Alltså är kolumnen Folkmängd fb av kombinationen Stad och Vara!

Det är ju lite fånigt, så därför definierar vi något som kallas fullständigt funktionellt beroende, som är ett funktionellt beroende där man inte kan ta bort några attribut ur determinanten om det fortfarande ska vara ett funktionellt beroende. Man kan också säga att determinanten är minimal.

I fortsättningen talar vi hela tiden om fullständiga funktionella beroenden, och när vi talar om en determinant menar vi en (eller flera) kolumner som en annan kolumn är ffb av.

I fortsättningen förkortar vi ibland "fullständigt funktionellt beroende" till "ffb".

Hur vet man vilka funktionella beroenden som finns?

Svaret är att det vet vi inte! Vilka beroenden som finns beror inte på vilka data som för tillfället råkar finnas i tabellen, utan det beror på logiken bakom tabellen.

Däremot kan man se vilka ffb som kan finnas, genom att de inte motsägs av de data som finns i tabellen.

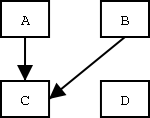
Alltså A -> C och B -> C.

Exempelvis kan det inte finnas ett ffb A -> B, eftersom det för samma värde på A (nämligen 2) förekommer olika värden på B (5 och 6).

Tänk på att determinanter kan vara sammansatta av flera attribut. I exemplet ovan finns det dock inga sådana ffb. Exempelvis kan det inte finnas ett ffb (A, B) -> D, eftersom det för samma värde på (A, B) förekommer olika värden på D. Det kan inte heller finnas ett ffb (B, D) -> C, men det beror på att det finns ett ffb B -> C, och alltså är (B, D) -> C visserligen ett funktionellt beroende, men inte ett fullständigt sådant.

Andra normalformen, "2NF" (ett första, dåligt, försök)

Detta är uppenbarligen en dum design, och mot just den här sortens dumma design hjälper andra normalformen.

Andra normalformen säger att en tabell, förutom att vara i första normalformen, inte får innehålla några fullständiga funktionella beroenden på delar av primärnyckeln. Om man ritar upp de fullständiga funktionella beroendena mellan attributen, får det alltså inte finnas några pilar från delar av primärnyckeln, bara från hela primärnyckeln.

• Definition av icke-nyckelattribut: Ett icke-nyckelattribut är ett attribut som inte ingår i primärnyckeln.
• Ett första försök till en definition av 2NF: 1NF, plus att varje icke-nyckelattribut ska vara ffb av hela primärnyckeln.

• Leverantör -> Stad
• Leverantör -> Folkmängd

En ny tabell Inköp (tabell 3), där Vara och Leverantör fortfarande är primärnyckel:

Och en tabell Leverantör (tabell 4), med Leverantör som primärnyckel. (Kanske vill man byta namn på kolumnen Leverantör till Namn, för det är ju namnet på leverantören, inte leverantörens leverantör.)

Dessa tabeller uppfyller 2NF. Nu står det bara på ett ställe att Saab ligger i Södertälje. Vi kan lägga in Gnesta-Kurres korvkiosk som leverantör, trots att vi ännu inte köper några varor därifrån.

Redundans i alla fall?

Inköp (tabell 5)

Leverantör (tabell 6)

En bättre definition av 2NF

Men det kan ju finnas flera kandidatnycklar i en tabell. I så fall måste vi tänka på alla kandidatnycklarna och inte bara primärnyckeln, om vi verkligen ska få bort de problem som 2NF ska lösa.

Det kan vi se genom ett exempel. Antag att vi inför ett unikt nummer på varje inköpssamband, och lägger till det som en kolumn i den ursprungliga tabellen Inköp (tabell 1). Då blir det numret en kandidatnyckel, förutom kombinationen av Vara och Leverantör. Tabell 7:

Om vi väljer kombinationen Vara och Leverantör som primärnyckel, precis som förut, så går det bra. Tabellen uppfyller inte 2NF, och måste delas upp. Men om vi väljer attributet Nummer som primärnyckel, så kommer tabellen att vara i 2NF redan från början! Alla icke-nyckelattributen är ju beroende av hela primärnyckeln. (Något annat vore konstigt, eftersom primärnyckeln inte är sammansatt!) Alla problemen, till exempel med redundans, kvarstår, trots att tabellen är i 2NF.

Därför vill vi ha en definition av 2NF som fungerar även med flera kandidatnycklar:

• Bättre definition av icke-nyckelattribut: Ett icke-nyckelattribut är ett attribut som inte ingår någon kandidatnyckel.
• Bättre definition av 2NF: 1NF, plus att varje icke-nyckelattribut ska vara ffb av varje kandidatnyckel.

Tredje normalformen, "3NF"

Tredje normalformen säger att en tabell, förutom att vara i andra normalformen, inte får innehålla några transitiva beroenden till icke-nyckelattribut. Det får alltså inte finnas några pilar som går mellan attribut utanför de olika kandidatnycklarna, bara (antingen) från kandidatnycklar till attributen utanför, eller från attributen utanför in i kandidatnycklarna. (Det betyder att om man har en sammansatt primärnyckel, så kan man ha pilar som pekar på ett av attributen i nyckeln.)

• Definition av 3NF: 2NF, plus att inget icke-nyckelattribut får vara ffb av något annat icke-nyckelattribut.

En ny tabell Leverantör (tabell 8), med attributet Leverantör som primärnyckel:

En tabell Stad (tabell 9), med attributet Stad som primärnyckel:

Dessa tabeller uppfyller 3NF.

Hur vet man hur man ska göra uppdelningen?

En ny tabell Leverantör (tabell 10), med attributet Leverantör som primärnyckel:

Och en tabell Stad (tabell 11), också med attributet Leverantör som primärnyckel! I den tabellen kan man läsa hur stor folkmängden är i den stad som en viss leverantör finns i:

Dessa tabeller uppfyller också 3NF! Det finns ju inga transitiva beroenden. Men uppenbarligen var det en ganska korkad uppdelning. Alla problemen som vi försökte lösa med hjälp av 3NF finns kvar.

Regel: Låt därför bli att göra korkade uppdelningar. Tänk på vad tabellerna betyder.

En ännu dummare uppdelning vore den här (tabell 12 och 13):

Tabellerna uppfyller 3NF, men med de här två tabellerna kan vi inte återskapa informationen i den ursprungliga leverantörstabellen. Vi vet inte vilken folkmängd som hör till vilken stad. Rader i tabellerna i en relationsdatabas har ju ingen bestämd ordning, så vi vet inte om 80000 hör ihop med Torslanda eller Södertälje.

Regel: Låt också bli att göra ännu dummare uppdelningar.

Boyce-Codds normalform, "BCNF"

• Krånglig definition av BCNF: 3NF, plus att inte heller nyckelattribut får vara ffb av icke-nyckelattribut.

Den stora fördelen med BCNF är nog att definitionen är enkel:

• Enkel definition av BCNF: 1NF, plus att varje determinant ska vara en kandidatnyckel.

Här är ett exempel på en tabell (tabell 14) som är i 3NF men inte i BCNF. Tabellen används för att lagra längden på svenska gator. Gatunamn är unika i varje stad, men inte i hela Sverige. Det kan alltså inte finnas två Storgatan i Gnesta, men det kan finnas en i Gnesta och en i Linköping. Det kan finnas flera postnummerområden i en ort.

Det finns två kandidatnycklar, som båda består av två attribut. Den ena är Gatunamn och Postnummer. Den andra är Gatunamn och Ortsnamn.

Tabellen innehåller följande fullständiga funktionella beroenden:

• Gatunamn, Postnummer -> Längd
• Gatunamn, Ortsnamn -> Längd
• Gatunamn, Ortsnamn -> Postnummer
• Postnummer -> Ortsnamn

Dela upp tabellen i två: dels en tabell med gator (tabell 15), dels en tabell med postnummerområden (tabell 16).

Ännu fler normalformer

Ibland är det bra att inte normalisera

Ett annat skäl till att välja en lägre normaliseringsgrad är prestanda. Om man har höga krav på att sökningar ska gå snabbt, bör man tänka på att det normalt tar längre tid för databashanteraren att söka i flera tabeller än i en enda tabell. När man delat upp en tabell i två, som vi visat tidigare, så måste databashanteraren joina ihop de två tabellerna för att återskapa den ursprungliga tabellen.

Regel: Använd därför teorin med förnuft. Ibland är det bra att inte normalisera. Men om du väljer en lägre normaliseringsgrad bör du ha goda skäl till det, och du bör vara medveten om vilka problem som kan uppstå. När du dokumenterar ditt system bör du sedan ange att du valt en lägre normaliseringsgrad, varför du gjorde det, och vilka problem du förutsett.

Inte bara för relationsmodellen

De viktigaste begreppen

normalform, normalisering, redundans, första normalformen (1NF), andra normalformen (2NF), tredje normalformen (3NF), Boyce-Codds normalform (BCNF), funktionellt beroende (fb), fullständigt funktionellt beroende (ffb)

Litteratur

• Padron-McCarthy/Risch, kapitel 11
• Connolly et al, fjärde upplagan: kapitel 13 och 14
• Date, åttonde upplagan: kapitel 11-13
• Elmasri/Navathe, fjärde upplagan: kapitel 14 och 15
• Silberschatz, fjärde upplagan: kapitel 7