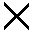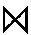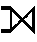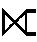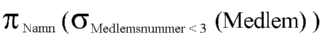Lecture Notes: Relational Algebra
Det finns inget kapitel om relationsalgebra i kursen.
Jag hade först tänkt ha med ett, men relationsalgebra passar
inte riktigt i en grundkurs som den här.
I stället finns en kort förklaring i ordlistan,
och för den som vill läsa mer finns dessutom dessa föreläsningsanteckningar
på engelska.
What? Why?
- Similar to normal algebra (as in 2+3*x-y), except we use relations as values instead of numbers, and the operations and operators are different.
- Not used as a query language in actual DBMSs. (SQL instead.)
- The inner, lower-level operations of a relational DBMS are, or are similar to, relational algebra operations.
We need to know about relational algebra to understand query execution and optimization in a relational DBMS.
- Some advanced SQL queries requires explicit relational algebra operations,
most commonly outer join.
- Relations are seen as sets of tuples, which means that no duplicates are allowed. SQL behaves differently in some cases. Remember the SQL keyword distinct.
- SQL is declarative,
which means that you tell the DBMS what you want,
but not how it is to be calculated.
A C++ or Java program is procedural,
which means that you have to state, step by step,
exactly how the result should be calculated.
Relational algebra is (more) procedural than SQL.
(Actually, relational algebra is mathematical expressions.)
Set operations
Relations in relational algebra are seen as sets of tuples,
so we can use basic set operations.
Review of concepts and operations from set theory
- set
- element
- no duplicate elements (but: multiset = bag)
- no order among the elements (but: ordered set)
- subset
- proper subset (with fewer elements)
- superset
- union
- intersection
- set difference
- cartesian product
Projection
Example: The table E (for EMPLOYEE)
| nr | name | salary |
|---|
| 1 | John | 100 |
| 5 | Sarah | 300 |
| 7 | Tom | 100 |
| SQL | Result | Relational algebra |
|---|
select salary
from E
|
|
PROJECTsalary(E)
|
select nr, salary
from E
|
|
PROJECTnr, salary(E)
|
Note that there are no duplicate rows in the result.
Selection
The same table E (for EMPLOYEE) as above.
| SQL | Result | Relational algebra |
|---|
select *
from E
where salary < 200
|
| nr | name | salary |
|---|
| 1 | John | 100 |
| 7 | Tom | 100 |
|
SELECTsalary < 200(E)
|
select *
from E
where salary < 200
and nr >= 7
|
|
SELECTsalary < 200 and nr >= 7(E)
|
Note that the select operation in relational
algebra has nothing to do with the SQL keyword select.
Selection in relational algebra returns those tuples in a relation
that fulfil a condition,
while the SQL keyword select
means "here comes an SQL statement".
Relational algebra expressions
| SQL | Result | Relational algebra |
|---|
select name, salary
from E
where salary < 200
|
| name | salary |
|---|
| John | 100 |
| Tom | 100 |
|
PROJECTname, salary
(SELECTsalary < 200(E))
or, step by step, using an intermediate result
Temp <- SELECTsalary < 200(E)
Result <- PROJECTname, salary(Temp)
|
Notation
The operations have their own symbols.
The symbols are hard to write in HTML that works with all browsers,
so I'm writing PROJECT etc here.
The real symbols:
| Operation | My HTML | Symbol |
|---|
| Projection | PROJECT |  |
| Selection | SELECT |  |
| Renaming | RENAME |  |
| Union | UNION |  |
| Intersection | INTERSECTION |  |
| Assignment | <- |  |
|
|
| Operation | My HTML | Symbol |
|---|
| Cartesian product | X | 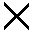 |
| Join | JOIN |  |
| Left outer join | LEFT OUTER JOIN | 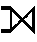 |
| Right outer join | RIGHT OUTER JOIN | 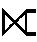 |
| Full outer join | FULL OUTER JOIN |  |
| Semijoin | SEMIJOIN | 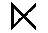 |
|
Example: The relational algebra expression which I would here write as
PROJECTNamn ( SELECTMedlemsnummer < 3 ( Medlem ) )
should actually be written
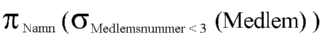
Cartesian product
The cartesian product of two tables combines
each row in one table with each row in the other table.
Example: The table E (for EMPLOYEE)
| enr | ename | dept |
|---|
| 1 | Bill | A |
| 2 | Sarah | C |
| 3 | John | A |
Example: The table D (for DEPARTMENT)
| dnr | dname |
|---|
| A | Marketing |
| B | Sales |
| C | Legal |
| SQL | Result | Relational algebra |
|---|
select *
from E, D
|
| enr | ename | dept | dnr | dname |
|---|
| 1 | Bill | A | A | Marketing |
| 1 | Bill | A | B | Sales |
| 1 | Bill | A | C | Legal |
| 2 | Sarah | C | A | Marketing |
| 2 | Sarah | C | B | Sales |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
| 3 | John | A | B | Sales |
| 3 | John | A | C | Legal |
|
E X D
|
- Seldom useful in practice.
- Usually an error.
- Can give a huge result.
Join (sometimes called "inner join")
The cartesian product example above combined
each employee with each department.
If we only keep those lines where the dept
attribute for the employee is equal to the dnr
(the department number) of the department,
we get a nice list of the employees,
and the department that each employee works for:
| SQL | Result | Relational algebra |
|---|
select *
from E, D
where dept = dnr
|
| enr | ename | dept | dnr | dname |
|---|
| 1 | Bill | A | A | Marketing |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
|
SELECTdept = dnr
(E X D)
or, using the equivalent join operation
E JOINdept = dnr D
|
- A very common and useful operation.
- Equivalent to a cartesian product followed by a select.
- Inside a relational DBMS, it is usually much more efficient
to calculate a join directly,
instead of calculating a cartesian product and then throwing away
most of the lines.
- Note that the same SQL query can be translated to several
different relational algebra expressions,
which all give the same result.
-
If we assume that these relational algebra expressions are executed,
inside a relational DBMS which uses relational algebra operations
as its lower-level internal operations,
different relational algebra expressions can take very different
time (and memory) to execute.
Natural join
A normal inner join, but using the join condition that columns with the same names
should be equal. Duplicate columns are removed.
Renaming tables and columns
Example: The table E (for EMPLOYEE)
| nr | name | dept |
|---|
| 1 | Bill | A |
| 2 | Sarah | C |
| 3 | John | A |
Example: The table D (for DEPARTMENT)
| nr | name |
|---|
| A | Marketing |
| B | Sales |
| C | Legal |
We want to join these tables, but:
- Several columns in the result will have the same name
(nr and name).
- How do we express the join condition,
when there are two columns called nr?
Solutions:
-
Rename the attributes, using the rename operator.
-
Keep the names, and prefix them with the table name, as is done in SQL.
(This is somewhat unorthodox.)
| SQL | Result | Relational algebra |
|---|
select *
from E as E(enr, ename, dept),
D as D(dnr, dname)
where dept = dnr
|
| enr | ename | dept | dnr | dname |
|---|
| 1 | Bill | A | A | Marketing |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
|
(RENAME(enr, ename, dept)(E))
JOINdept = dnr
(RENAME(dnr, dname)(D))
|
select *
from E, D
where dept = D.nr
|
| nr | name | dept | nr | name |
|---|
| 1 | Bill | A | A | Marketing |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
|
E JOINdept = D.nr D
|
You can use another variant of the renaming operator
to change the name of a table, for example to
change the name of E to R.
This is necessary when joining a table with itself (see below).
RENAMER(E)
A third variant lets you rename both the table and the columns:
RENAMER(enr, ename, dept)(E)
Aggregate functions
Example: The table E (for EMPLOYEE)
| nr | name | salary | dept |
|---|
| 1 | John | 100 | A |
| 5 | Sarah | 300 | C |
| 7 | Tom | 100 | A |
| 12 | Anne | null | C |
| SQL | Result | Relational algebra |
|---|
select sum(salary)
from E
|
|
Fsum(salary)(E)
|
Note:
- Duplicates are not eliminated.
- Null values are ignored.
| SQL | Result | Relational algebra |
|---|
select count(salary)
from E
|
Result:
|
Fcount(salary)(E)
|
select count(distinct salary)
from E
|
Result:
|
Fcount(salary)(PROJECTsalary(E))
|
You can calculate aggregates "grouped by" something:
| SQL | Result | Relational algebra |
|---|
select sum(salary)
from E
group by dept
|
|
deptFsum(salary)(E)
|
Several aggregates simultaneously:
| SQL | Result | Relational algebra |
|---|
select sum(salary), count(*)
from E
group by dept
|
|
deptFsum(salary), count(*)(E)
|
Standard aggregate functions:
sum, count, avg, min, max
Hierarchies
Example: The table E (for EMPLOYEE)
| nr | name | mgr |
|---|
| 1 | Gretchen | null |
| 2 | Bob | 1 |
| 5 | Anne | 2 |
| 6 | John | 2 |
| 3 | Hulda | 1 |
| 4 | Hjalmar | 1 |
| 7 | Usama | 4 |
Going up in the hierarchy one level:
What's the name of John's boss?
| SQL | Result | Relational algebra |
|---|
select b.name
from E p, E b
where p.mgr = b.nr
and p.name = "John"
|
|
PROJECTbname
([SELECTpname = "John"(RENAMEP(pnr, pname, pmgr)(E))]
JOINpmgr = bnr
[RENAMEB(bnr, bname, bmgr)(E)])
or, in a less wide-spread notation
PROJECTb.name
([SELECTname = "John"(RENAMEP(E))]
JOINp.mgr = b.nr
[RENAMEB(E)])
or, step by step
P <- RENAMEP(pnr, pname, pmgr)(E)
B <- RENAMEB(bnr, bname, bmgr)(E)
J <- SELECTname = "John"(P)
C <- J JOINpmgr = bnr B
R <- PROJECTbname(C)
|
Notes about renaming:
-
We are joining E with itself,
both in the SQL query and in the relational algebra expression:
it's like joining two tables with the same name and the same attribute names.
-
Therefore, some renaming is required.
-
RENAMEP(E)
JOIN...
RENAMEB(E)
is a start, but then we still have the same attribute names.
Going up in the hierarchy two levels:
What's the name of John's boss' boss?
| SQL | Result | Relational algebra |
|---|
select ob.name
from E p, E b, E ob
where b.mgr = ob.nr
where p.mgr = b.nr
and p.name = "John"
|
|
PROJECTob.name
(([SELECTname = "John"(RENAMEP(E))]
JOINp.mgr = b.nr
[RENAMEB(E)])
JOINb.mgr = ob.nr
[RENAMEOB(E)])
or, step by step
P <- RENAMEP(pnr, pname, pmgr)(E)
B <- RENAMEB(bnr, bname, bmgr)(E)
OB <- RENAMEOB(obnr, obname, obmgr)(E)
J <- SELECTname = "John"(P)
C1 <- J JOINpmgr = bnr B
C2 <- C1 JOINbmgr = bbnr OB
R <- PROJECTobname(C2)
|
Recursive closure
Both one and two levels up:
What's the name of John's boss,
and of John's boss' boss?
| SQL | Result | Relational algebra |
|---|
(select b.name ...)
union
(select ob.name ...)
|
|
(...)
UNION
(...)
|
Recursively:
What's the name of all John's bosses?
(One, two, three, four or more levels.)
-
Not possible in (conventional) relational algebra,
but a special operation called transitive closure
has been proposed.
-
Not possible in (standard) SQL (SQL2),
but in SQL3, and using SQL + a host language with loops or recursion.
Outer join
Example: The table E (for EMPLOYEE)
| enr | ename | dept |
|---|
| 1 | Bill | A |
| 2 | Sarah | C |
| 3 | John | A |
Example: The table D (for DEPARTMENT)
| dnr | dname |
|---|
| A | Marketing |
| B | Sales |
| C | Legal |
List each employee together with the department he or she works at:
| SQL | Result | Relational algebra |
|---|
select *
from E, D
where edept = dnr
or, using an explicit join
select *
from (E join D on edept = dnr)
|
| enr | ename | dept | dnr | dname |
|---|
| 1 | Bill | A | A | Marketing |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
|
E JOINedept = dnr D
|
No employee works at department B, Sales,
so it is not present in the result.
This is probably not a problem in this case.
But what if we want to know the number of employees at each department?
| SQL | Result | Relational algebra |
|---|
select dnr, dname, count(*)
from E, D
where edept = dnr
group by dnr, dname
or, using an explicit join
select dnr, dname, count(*)
from (E join D on edept = dnr)
group by dnr, dname
|
| dnr | dname | count |
|---|
| A | Marketing | 2 |
| C | Legal | 1 |
|
dnr, dnameFcount(*)(E JOINedept = dnr D)
|
No employee works at department B, Sales,
so it is not present in the result.
It disappeared already in the join,
so the aggregate function never sees it.
But what if we want it in the result,
with the right number of employees (zero)?
Use a right outer join,
which keeps all the rows from the right table.
If a row can't be connected to any of the rows from the left table
according to the join condition, null values are used:
| SQL | Result | Relational algebra |
|---|
select *
from (E right outer join D on edept = dnr)
|
| enr | ename | dept | dnr | dname |
|---|
| 1 | Bill | A | A | Marketing |
| 2 | Sarah | C | C | Legal |
| 3 | John | A | A | Marketing |
| null | null | null | B | Sales |
|
E RIGHT OUTER JOINedept = dnr D
|
select dnr, dname, count(*)
from (E right outer join D on edept = dnr)
group by dnr, dname
|
| dnr | dname | count |
|---|
| A | Marketing | 2 |
| B | Sales | 1 |
| C | Legal | 1 |
|
dnr, dnameFcount(*)(E RIGHT OUTER JOINedept = dnr D)
|
select dnr, dname, count(enr)
from (E right outer join D on edept = dnr)
group by dnr, dname
|
| dnr | dname | count |
|---|
| A | Marketing | 2 |
| B | Sales | 0 |
| C | Legal | 1 |
|
dnr, dnameFcount(enr)(E RIGHT OUTER JOINedept = dnr D)
|
Join types:
- JOIN = "normal" join = inner join
- LEFT OUTER JOIN = left outer join
- RIGHT OUTER JOIN = right outer join
- FULL OUTER JOIN = full outer join
Outer union
Outer union
can be used to calculate the union
of two relations that are partially union compatible.
Not very common.
Example: The table R
Example: The table S
The result of an outer union between R and S:
Division
Who works on (at least) all the projects that Bob works on?
Semijoin
A join where the result only contains the columns from one of the joined tables.
Useful in distributed databases,
so we don't have to send as much data over the network.
Update
To update a named relation, just give the variable a new value.
To add all the rows in relation N to the relation R:
R <- R UNION N