|
Det här är ett avsnitt i en
webbkurs om databaser
som finns fritt tillgänglig på adressen
http://www.databasteknik.se/webbkursen/.
Senaste ändring:
20 februari 2020.
Av Thomas Padron-McCarthy. Copyright, alla rättigheter reserverade, osv. Skicka gärna kommentarer till webbkursen@databasteknik.se.
|
Det här avsnittet är tänkt som en kort introduktion till lagringsstrukturer, för den som inte kan så mycket innan. Webbkursen om databaser handlar ju mest om användning av databaser, men det här avsnittet är tänkt som en hjälp om man senare ska lära sig hur databaser fungerar inuti.
Ibland menar man med variabel en plats i minnet som har ett eget namn, men i det här avsnittet använder vi alltså uttrycket i den mer allmänna betydelsen "en viss plats i minnet".
Exempel på en post med tre fält:

När en tabell i en relationsdatabas ska hanteras internt av en databashanterare, kan det hända att varje rad lagras som en post.
Exempel på en array med tre heltal, där man låtit det första elementet få positionsnummer 1:
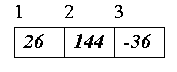
Om vi vet positionsnumret för ett element i arrayen, kan vi komma åt det direkt. Vi behöver alltså inte leta igenom arrayen, eller stega igenom de element som ligger före.
Man kan också ha arrayer av poster. Här är ett exempel på en array med fyra poster, där man låtit den första posten få positionsnummer 0:
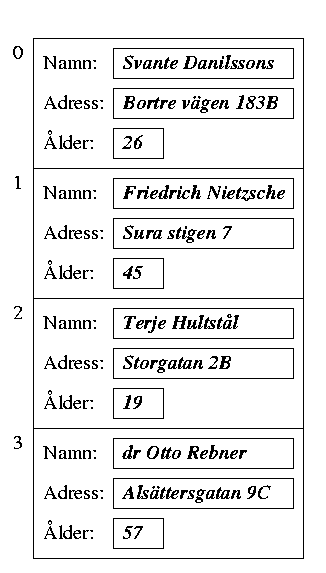
En tabell i en relationsdatabas skulle kunna lagras internt i databashanteraren som en array av poster, även om det kanske inte är så vanligt i praktiken.
Här har vi en pekarvariabel som heter "p", och som innehåller ett pekarvärde som pekar ut en post:
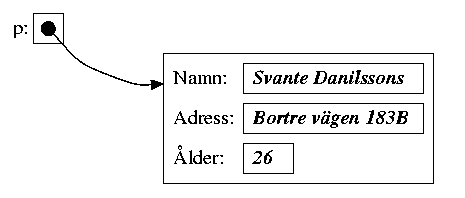
Vi kan inte komma åt posten direkt, utan det enda sättet att hitta den är att följa pekaren till den.
För det mesta när man talar om pekare så menar man primärminnespekare, som pekar ut en plats i datorns primärminne. Men det finns också diskpekare, som pekar ut en plats på hårddisken.
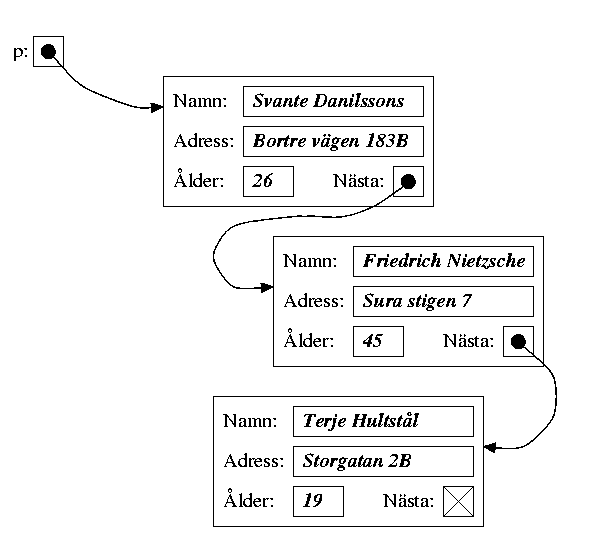
Den sista posten i den länkade listan har en så kallad null-pekare eller nil-pekare i sitt Nästa-fält, för att markera att listan tar slut där. En null-pekare är ett speciellt pekarvärde som betyder att den pekaren inte pekar på något alls.
Vi kan inte komma åt en post i listan direkt, utan det enda sättet att hitta den är att gå igenom listan genom att följa pekarna, post för post, tills vi kommer fram till den sökta posten.
I en länkad lista gick det inte lika lätt. För att komma åt en viss post måste vi gå igenom listan genom att följa pekarna, post för post, tills vi kommer fram till den sökta posten. Det kallas sekvensiell åtkomst ("sequential access" på engelska).
Om vi söker i en sådan osorterad lagringsstruktur, till exempel för att hitta en post som innehåller namnet "Friedrich Nietzsche", måste vi gå igenom lagringsstrukturen post för post. Det gäller både för arrayen och för listan. Arrayens möjlighet till direkt åtkomst ger alltså ingen fördel i det här fallet.
Om vi vet att namn är unika, kan vi förstås sluta leta när vi hittat den av posterna som innehåller namnet "Friedrich Nietzsche". I så fall räcker det med att, i genomsnitt, leta igenom hälften av posterna (under förutsättning att det sökta namnet finns där). Om namn inte är unika, och vi vill hitta alla de poster som innehåller "Friedrich Nietzsche", måste vi förstås leta igenom alla posterna.
Sökning i osorterade lagringsstrukturer av alla slag kräver att man letar igenom alla posterna, eller (under vissa förutsättningar) i genomsnitt hälften av dem. Vi säger att tiden för sökning är proportionell mot n, där n är antalet poster. Om antalet poster blir dubbelt så stort, tar det dubbelt så lång tid. Om antalet poster blir tusen gånger så stort, tar det tusen gånger så lång tid.
Binärsökning går till så att man tar posten mitt i arrayen, och jämför med det sökta namnet. Om den mittersta postens namn kommer före det sökta namnet i bokstavsordning, vet vi nu att den sökta posten finns i andra halvan av arrayen. Om den mittersta postens namn i stället kommer efter det sökta namnet i bokstavsordning, vet vi nu att den sökta posten finns i första halvan av arrayen.
Sen fortsätter man på samma sätt med den mittersta posten i den ena halvan av arrayen, och så vidare tills man antingen hittar den sökta posten, eller tills man halverat arrayen så många gånger att intervallet man tittar på är mindre än en post. I så fall fanns den sökta posten inte i arrayen.
Lite matematik ger att sökning i sorterade lagringsstrukturer med direkt åtkomst i genomsnitt kräver att man tittar i ett antal poster som är lika med 2-logaritmen av antalet poster. Vi säger att tiden för sökning är proportionell mot 2-logaritmen för n, där n är antalet poster. Om antalet poster blir dubbelt så stort, behöver vi göra en halvering till, och alltså titta på en post till. Om antalet poster blir tusen gånger så stort, behöver vi göra tio halveringar till (210 = 1024, vilket är mer än 1000), och alltså titta på tio poster till.
Notera att om man multiplicerar antalet poster med något, så behöver man inte multiplicera söktiden med något, utan man ska addera något till söktiden.
En liten vinst får vi dock, jämfört med osorterade sekvens-åtkomst-strukturer. Om vi letar efter en post som inte finns i listan, kan vi sluta leta när vi passerat den plats i listan där posten skulle ha funnits.
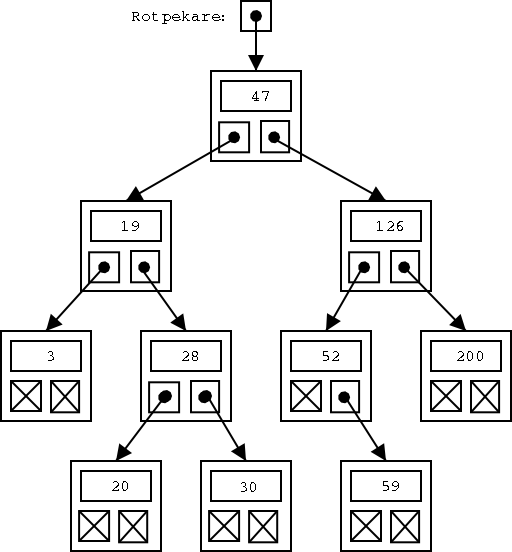
I det här exemplet innehåller varje post bara ett fält, nämligen ett nummer, men man kan förstås ha fler fält, till exempel namn och adress. Posterna i trädet brukar kallas noder. Notera att träd i datasammanhang brukar ritas upp och ned, med roten högst upp! Trädets rot utgörs av den så kallade rot-noden, den med värdet 47 i figuren. Trädet i figuren har djupet 4, eftersom det finns fyra nivåer av noder. (Egentligen borde det nog heta "höjden", men eftersom man ritar träden upp och ner brukar man kalla det för "djup".)
I ett binärt träd har varje nod två "under-träd". Ett eller båda under-träden kan vara tomma, vilket i figuren anges med null-pekare. Ibland kallas noderna som bara har tomma under-träd för löv-noder eller bara löv. (Och löven finns alltså längst ner i datavetenskapens träd.)
Alla noder måste ha ett unikt värde på det fält vi använder för att söka på. Vi brukar kalla det för en nyckel eller (när man söker på det) en söknyckel.
Om vi tittar på en nod i trädet (till exempel rot-noden), ser vi att alla posterna i det vänstra under-trädet har nyckelvärden som är mindre. 3, 19, 20, 28 och 30 är ju alla mindre än 47. Vi ser också att alla posterna i det högra under-trädet har nyckelvärden som är större. 52, 59, 126 och 200 är ju alla större än 47.
Det kan vi utnyttja när vi söker i trädet. Antag att vi letar efter posten med värdet 20. Vi börjar med att titta på rot-noden, som har värdet 47. 20 är mindre än 47, så vi vet att den sökta posten (med värde 20) måste ligga till vänster. Alltså följer vi den vänstra vidare-pekaren, till noden med värde 19.
20 är större än 19, så vi vet att den sökta posten (med värde 20) måste ligga till höger. Alltså följer vi den högra vidare-pekaren, till noden med värde 28.
20 är mindre än 28, så vi vet att den sökta posten (med värde 20) måste ligga till vänster. Alltså följer vi den vänstra vidare-pekaren, till noden med värde 20. Och då har vi hittat den sökta noden.
Sökning i ett binärt träd påminner lite om binärsökning i en array, och precis som för binärsökning så är tiden för sökning proportionell mot 2-logaritmen för n, där n är antalet poster. (Detta beror dock lite på hur trädet ser ut.)
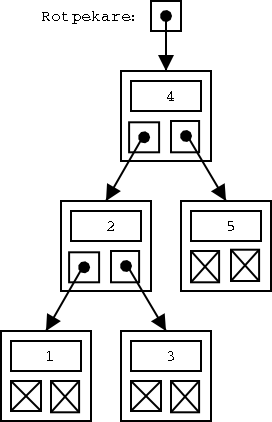
Ett (vanligt) binärt träd växer alltså genom att man skapar nya noder och sätter dit på de gamla lövnoderna. Den nya noden blir då lövnoden, och den gamla lövnoden blir en "inre" nod, dvs inte längre en lövnod.
|
|
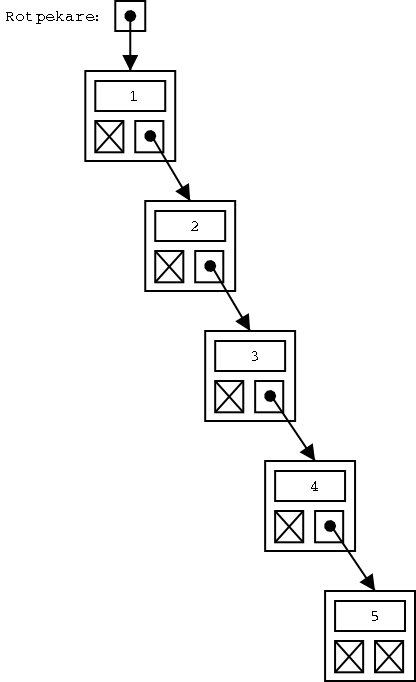
Som vi ser kan ett binärt träd i värsta fall urarta till en länkad lista med sorterade element. Trädet får alltså "en enda lång gren". Då får det lika dåliga sökegenskaper som en länkad lista. Lyckligtvis finns det metoder för att hålla binära träd balanserade, dvs "jämnhöga överallt": Noderna flyttas runt automatiskt allteftersom man stoppar in (eller tar bort) element.
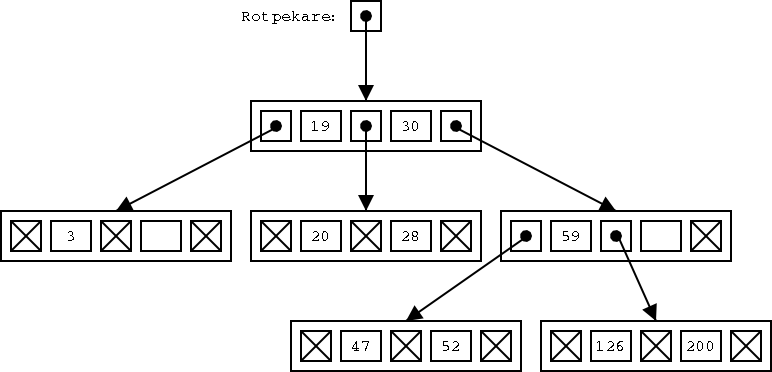
I ett träd av ordning tre innehåller varje nod plats för två dataelement. I exemplet har varje element ett fält, nämligen ett nummer, men man kan förstås ha fler fält, till exempel namn och adress. Det är alltså egentligen hela poster, som man stoppar in flera av i varje nod i trädet.
Som vi ser behöver inte alla noder innehålla två dataelement, utan det kan förekomma tomma datafält. (Det är ju egentligen självklart: Om antalet dataelement är udda, måste ju minst en nod innehålla ett tomt datafält.) Inte heller behöver alla noder verkligen ha tre underträd, utan de kan också ha noll, ett eller två underträd.
Sökning i ett träd av högre ordning än två påminner om sökning i ett binärt träd. Om vi tittar på rotnoden i vårt exempelträd, så ser vi att det innehåller dataelementen 19 och 30. Vi ser också att alla dataelementet i det vänstra under-trädet (som pekas ut av pekaren till vänster om 19) har nyckelvärden som är mindre än 19. Alla dataelement i det mellersta under-trädet (som pekas ut av pekaren mellan 19 och 30)) har nyckelvärden mellan 19 och 30. Alla dataelement i det högra under-trädet (som pekas ut av pekaren till höger om 30) har nyckelvärden som är större än 30.
Om vi letar efter dataelementet med värdet 52 börjar vi med att titta i rotnoden, och konstaterar att 52 är större än 30. Alltså finns 52 i det högra under-trädet. Vi följer pekaren till rot-noden i det under-trädet. Där ser vi att 52 är mindre än 59, och alltså måste det sökta dataelementet finnas i det vänstra under-trädet. Vi följer pekaren dit, och när vi tittar i den noden hittar vi 52.
Träd av högre ordning blir grundare än träd av lägre ordning. Man kan också säga att de blir "låga, breda och buskiga", jämfört med de "höga och smala" träden av lägre ordning. Eftersom träd av högre ordning blir grundare, måste man leta i färre noder vid sökning. Å andra sidan blir det lite mer arbete i varje nod.
Trädet av ordning 3 i exemplet ovan är inte ett B-träd. Det ser man på att alla lövnoder inte är på samma nivå. Här är ett B-träd av ordning 3, med samma tio dataelement:
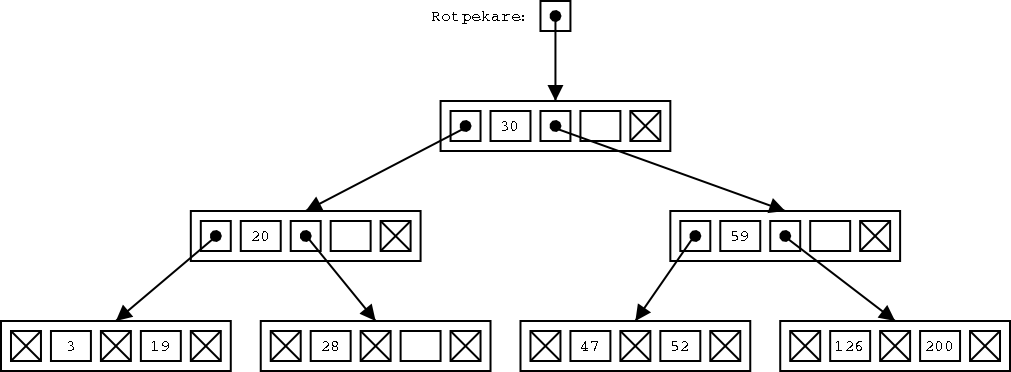
Om antalet poster blir dubbelt så stort, behöver vi (oftast) inte fler nivåer i trädet. Om antalet poster blir tio gånger så stort, behöver vi en nivå till. Om antalet poster blir tusen gånger så stort, behöver vi tre nivåer till (103 = 1000).
| Tro inte på mig! Jag ljuger! Det där är en förenkling, och alltså lögn. I verkligheten är ju inte alla noder alltid fulla. I genomsnitt är noderna i ett B-träd två tredjedels fulla. Den "effektiva ordningen" av ett B-träd av ordningen r blir alltså två tredjedelar av r. Dessutom är det bara ett genomsnitt, och noderna kan, som vi nämnde tidigare, vara allt från halvfulla till helt fulla. |
Som alltid med logaritmiska söktider gäller att när man multiplicerar antalet poster med något, så behöver man inte multiplicera söktiden med något, utan man ska addera något till söktiden.
Om det nu finns en tom plats i den noden, så är det bara att stoppa in det nya dataelementet där. Om vi till exempel vill sätta in 29, så ska det in i den andra lövnoden från vänster. Där finns en tom plats, så vi stoppar helt enkelt in det nya elementet där. Nu ser noden ut så här:

Men vad händer om noden redan är full? Antag att vi i stället ska stoppa in värdet 17. Rätt plats för det är lövnoden längst till vänster, men den är redan full. Då måste vi dela upp den i två genom att skapa en ny nod och fördela dataelementen på de två noderna:

Den nya noden måste ju ha en pekare till sig, precis som alla andra noder, så en pekare till den måste stoppas in i noden ovanför. För att ordningen på elementen ska stämma, dvs att vänster under-träd bara innehåller element som är mindre än det första dataelementet i en nod, och så vidare, måste vi flytta runt elementen lite mellan de tre inblandade noderna: den gamla lövnoden, den nya lövnoden, och noden ovanför. Nu ser det ut så här:
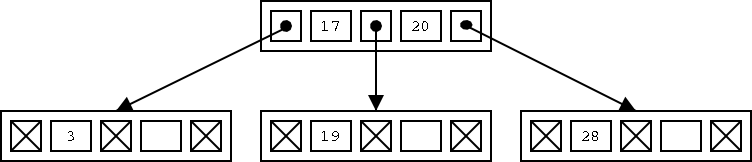
B-träd växer alltså inte genom att man sätter dit nya noder under lövnoderna, utan genom att lövnoder delar sig i två när de blir fulla.
Nu kan det hända att även noden ovanför lövnoden blir överfull. Om vi sätter in några nya dataelement (till exempel 5, 18 och 7) så kanske vi måste dela upp en lövnod till i det här delträdet i två. Då har vi plötsligt fyra lövnoder, som ska pekas ut med pekare. De fyra pekarna får inte plats i noden ovanför. Då får man dela upp den noden också i två, och flytta runt elementen, på samma sätt som när man delar upp en lövnod.
Det kan förstås hända att även nästa nod, på den tredje nivån nerifrån, blir överfull. Då måste den också delas. På så sätt kan "delningen" fortsätta upp genom hela B-trädet. Kanske kommer man hela vägen upp till rotnoden, och det visar sig att den också blir överfull. Då måste rotnoden också delas upp i två. Men man kan inte ha två rotnoder. Det skulle ju bli två skilda träd bredvid varandra. Därför skapar man en ny rotnod, och lägger in pekarna till de två under-träden i den.
Ett vanligt träd växer på höjden genom att man hakar på nya lövnoder under de gamla lövnoderna. Ett B-träd växer på höjden genom att man sätter dit en ny rotnod, ovanför den gamla rotnoden.
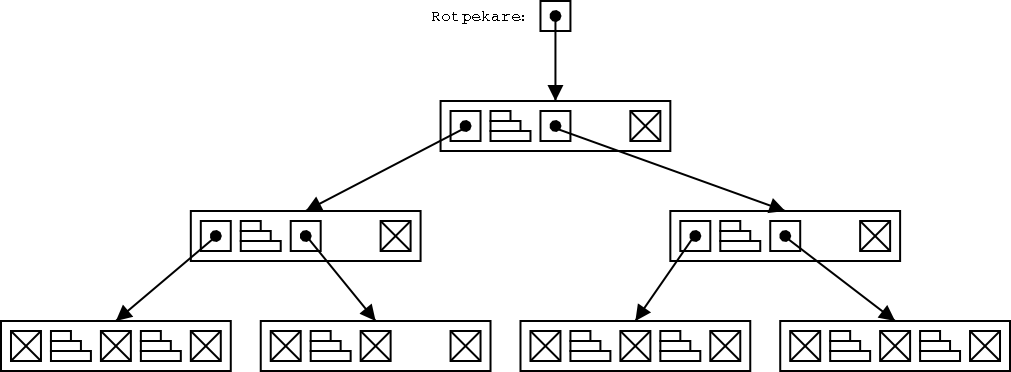
Om vi tittar på en enskild nod, så skulle man kunna rita upp den så här:

Om noderna är av en viss, bestämd storlek, så säger det sig självt att ju större posterna är, desto färre går det in i varje nod. Om man lät bli att ta med hela posterna, utan bara använde sig av själva söknyckeln, så skulle man få plats med fler dataelement och fler pekare:

(Nej, det går inte riktigt in ett heltal och en pekare längst till höger i figuren. Mät själv och se. Det blir alltså lite plats i noden som inte används.)
Trädet blir nu av ordningen 7 i stället för ordningen 3. Vi kommer ihåg sedan tidigare att ett träd av högre ordning blir lägre och bredare än ett träd av lägre ordning som innehåller samma data. Ett lägre och bredare träd har färre nivåer, och alltså är det färre noder man måste leta i för att hitta det element man söker.
Det här är principen bakom en variant på B-träd som kallas B+-träd (uttalas "be-plus-träd"). De riktiga posterna, med personernas namn och adress, måste ju finnas med någonstans, och dem lägger vi i lövnoderna. Lövnoderna innehåller alltså hela poster, och alla poster i trädet finns i lövnoderna. I de inre noderna, noderna ovanför lövnoderna, finns inte några hela poster, utan där använder vi enbart söknyckeln.

I det här exemplet hade B-trädet djupet 3, medan B+-trädet får höjden 2. I B+-trädet kan man alltså hitta vilken post som helst genom att undersöka bara två noder. (Det här är bara ett exempel. Ett B+-träd kan förstås ha fler än två nivåer.)
(Nej, dataposterna i lövnoderna har inte plötsligt blivit större. Jag bara ritade dem lite bredare, så noderna inte skulle se så tomma ut. Skalan blir lite konstig, eftersom dataposterna är ritade ungefär lika stora som pekarna. I verkligheten skullle dataposterna vara mycket större än pekarna.)
B+-träd är populära i databashanterare. De flesta vanliga databashanterare lagrar sina data på hårddiskar, och B+-träd är en bra datastruktur just för diskar. Diskar arbetar blockvis, så att man alltid läser ett helt diskblock (på några tusen byte) åt gången när man läser från disken. Även om man bara behöver en liten del av dessa data, läser man alltid ett helt block. Dessutom är diskar mycket långsamma jämfört med primärminne, så det tar jämförelsevis mycket lång tid att hämta data från disken. Därför vill man organisera sina datastrukturer så att data som hör ihop lagras tillsammans i varje diskblock, och att man därför inte behöver titta i så många olika diskblock. Både i B+-träd och i vanliga B-träd använder man hela diskblock som noder. Det går alltså in ganska många söknycklar och pekare i en nod. B+-träd av ordningen flera hundra är inget ovanligt. Eftersom varje nod kan ha flera hundra underträd, blir trädet mycket grunt, och man behöver inte titta i så många noder (läsa så många diskblock).
Alla poster ligger alltså på samma nivå i trädet, i lövnoderna, och dessutom är de sorterade i ordning. Om vi länkar ihop alla lövnoderna med pekare, i en länkad lista, blir det extra lätt att inte bara hitta en post med ett visst nyckelvärde, utan också att gå igenom alla posterna i sorteringsordningen:
Antag att vi har ett personregister. Varje person har ett nummer och ett namn. Vi lagrar personerna i en array av poster:
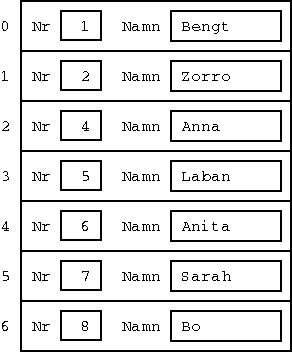
Om vi vill ha tag på en person med ett visst nummer, till exempel 7, får vi leta igenom arrayen sekvensiellt tills vi hittar rätt post. Om vi ser till att hålla posterna sorterade i nummerordning, kan vi använda binärsökning så att det går lite fortare.
Men vill vi att det ska gå riktigt snabbt, så kan vi placera varje post på samma arrayposition som personens nummer:
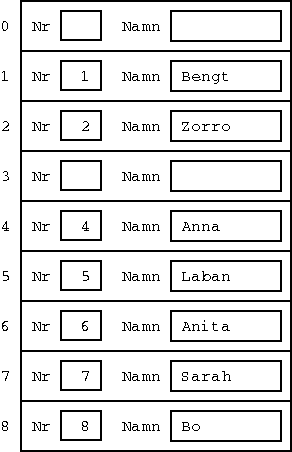
Om vi nu vill ha tag på personen med nummer 7, så är det bara att gå direkt till arrayposition nummer 7, och så finns posten där.
Sökningar går mycket snabbt med den här metoden, men det finns flera nackdelar:
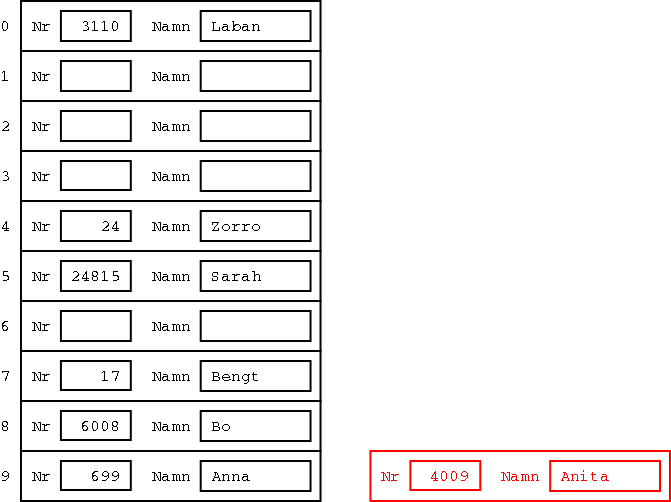
Om vi nu vill hitta posten med nummer 24, så tar vi entalssiffran av det, nämligen 4, och går direkt till position nummer 4 i arrayen. Där hittar vi rätt post. Vi behöver alltså inte leta i arrayen, utan vi går direkt till rätt ställe.
Men som den uppmärksamme läsaren kanske redan noterat så finns det ett problem. De två posterna med nummer 699 och nummer 4009 har båda nummer som slutar på 9, och hör båda hemma på arrayposition 9. Det kallas en kollision, och det finns flera olika metoder att lösa det på, så kallad kollisionshantering. Ett sätt är att stoppa in ett extra pekarfält i varje post, och sen bygga en länkad lista av alla de poster som ska finnas på en viss position i arrayen. De "extra" posterna får man då placera någon annanstans i minnet än i själva arrayen.
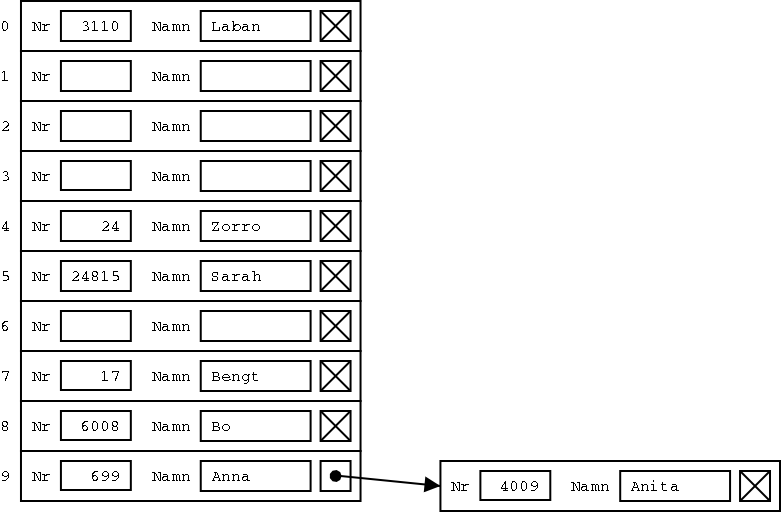
h(x) = x mod 10En hashfunktion gör alltså om ett sökvärde, till exempel ett stort tal, till ett positionsnummer, som är ett (förhållandevis) litet tal. Just den här modulo-10-funktionen är en ganska dålig hashfunktion. Vad händer till exempel om man använder den på folks löner? Väldigt många löner slutar på ett jämt hundratal, eller till och med tusental, och alla dessa skulle hamna på position noll i hashtabellen! Det kan vara bättre att att använda ett primtal som storlek på hashtabellen, och låta hashfunktionen beräkna modulo det primtalet.
Hashfunktioner som används i riktiga program kan vara betydligt mer komplicerade. Det är viktigt att hashfunktionen sprider olika värden på söknyckeln bra, så att posterna inte klumpar ihop sig på en eller en del av platserna i arrayen. Det finns också hashfunktioner som fungerar på textsträngar. Dessa hashfunktioner brukar använda teckenkoderna för de ingående tecknen i strängen, och slå ihop dem eller multiplicera dem med varandra på olika sätt.
Om antalet poster blir dubbelt så stort, tar sökningar fortfarande lika lång tid. Om antalet poster blir tusen gånger så stort, tar sökningar fortfarande lika lång tid.
Det där är lite för bra för att vara sant. Det finns två problem:
Ännu en nackdel är att vi, för att kunna beräkna hashfunktionen och därmed hitta en post, måste känna till hela söknyckeln. Om man ska söka efter Bengt Svenzon i en hashtabell måste man alltså känna till hela namnet, och hur det stavas. Det fungerar till exempel inte att söka efter alla namn som börjar med Bengt.
Det finns flera sätt att lösa problemet med hashtabeller som blir fulla:
|
Faktaruta:
När jag skriver det här (februari 2020) har en typisk modern persondator eller arbetsstation
ett primärminne på 8-64
gibibyte,
och ett diskutrymme på 1-2
terabyte.
En stor servermaskin kan ha mycket mer.
Hela den här webbdatabaskursen utgör just nu 1846895 byte, med bilder och allt. Kursen får alltså plats i primärminnet flera tusen gånger, och flera miljoner gånger på disken. Att hämta en uppgift var som helst i primärminnet tar omkring 7 ns (0.000000007 sekunder). Att hämta en uppgift var som helst på en mekanisk hårddisk tar i genomsnitt omkring 10 ms (0.01 sekunder). Disken är alltså ungefär en miljon gånger långsammare än primärminnet. En SSD är ungefär 100 gånger snabbare än en mekanisk hårddisk, men det är ändå 10000 gånger långsammare än primärminnet. |